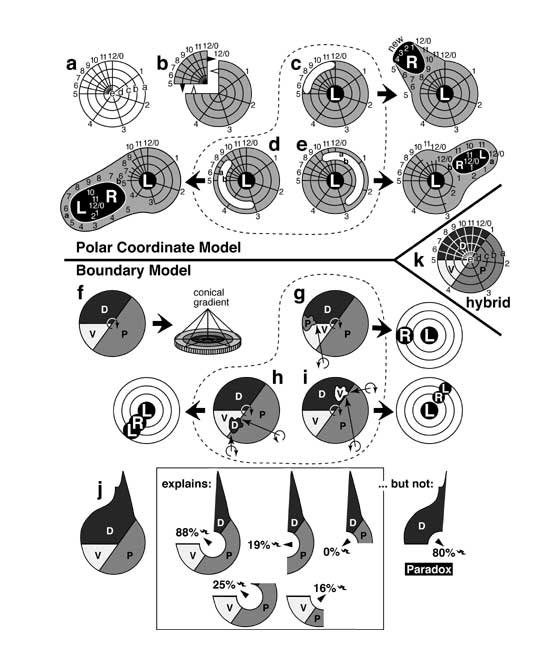
Figure 5.3
Models for pattern formation that were prominent in the 1980s, and how they explained regeneration-duplication phenomena in leg discs (cf. Fig. 5.2). In the Polar Coordinate (PC) Model (a-e) [1303] growth is supposedly stimulated when distant cells abut via healing, whereas in the Boundary Model (f-j) [2804, 2808] distal growth is provoked when three kinds of cells convene.

a. Polar coordinates in a left leg disc (cf. Fig. 4.6). Each cell assesses its position as (1) radial distance (lettered rings) from the center and (2) angular declination (numbered spokes) from an arbitrary radius (12/0). Unlike the wing disc where angular values are presumed to be spaced evenly, here they must be crowded since the upper medial (UM) quadrant regenerates.

b. In the PC Model, fragments (e.g., UM) with >50% of the angular values regenerate (black triangles), while pieces (e.g., 3/4 part) with <50% duplicate (hollow triangles). In each case, the edges (5 and 12/0) intercalate via the shortest route (cf. Fig. 4.6d).

c-e. Distal outgrowths can occur if tissue is lost from certain regions, and the edges of the hole (white 'sausages') heal as shown. c. If cells are lost from the UM perimeter, then an extra 'clockface' arises when new tissue (black) fills the 5-12/0 gap by the shorter route (viz. 1-4). Because the new clockface is backwards the outgrowth will be right-handed (R vs. L). Comparable losses from other peripheral parts should not form whole circles, which is problematic since mirror planes of twinned legs tend to be at right angles to spoke #4, not #8 [3442]. d. Loss of internal coordinates can generate two whole new circles if wound edges reorient (during evagination?) to abut values from >50% declination (e.g., 9 and 3; a and b = outer two rings) [1495]. e. Confrontations of <50% declination will form partial circles and stunted outgrowths. L-R-L handedness (d, e) obeys Bateson's Rule (see text), but the model doesn't explain why converging outgrowths (e) occur near angular value #1 (cf. Fig. 5.2c) and not near #2-4.

f. In Meinhardt's Boundary Model, the anterior compartment is subdivided into ventral (V) and dorsal (D) parts, while the posterior (P) compartment is not. The PVD sequence is clockwise in left legs (curved arrow). Each cell identity -- P, V, or D -- furnishes one key ingredient for making a morphogen. The morphogen is created only at the nexus, and its diffusion forms a conical gradient (rings = contours; epithelium in side view).

g-i. The model explains outgrowths. g. Duplications arise when a peripheral patch that straddles a boundary (e.g., D/V) transforms into the third type (P), thus creating a new PVD nexus (arrow) that grows out to form a right limb. h. If such a patch is internal, then limbs arise at two new PVD points. i. If the patch merely touches a border, then too little morphogen may be made to sustain two tips, in which case the outgrowth converges. As for why ventral outgrowths diverge and dorsal ones converge (cf. Fig. 5.2c), the model must assume (ad hoc) that D spots tend to straddle P/V (h), while V spots only touch D/P (i).

j. The model (in a leg disc at left) explains most surgical outcomes. When the boxed fragments are cultured, they regenerate claws (bicurved symbol) and other distal structures that map in the excised endknob at frequencies indicated. Regenerative ability is maximal when all 3 domains remain (88%), as expected. However, the model doesn't explain why the UM quadrant (sans endknob) also replaces claws often [2804].

k. Hybrid PC-Boundary Model, where P/V, V/D, and D/P radii specify angular values (4, 5, 1) in a PC system [2808].

Panels a and b are redrawn from [1303] (angular spacing was later revised [4140]); c-e are adapted from [1495, 1496, 3442]; f-k are based on [2804, 2808] (he uses AD and AV, not D and V); data in j are from [3811, 4140]. See also App. 7.